Detecção de anomalias em séries temporais

Como identificar padrões incomuns em dados, que podem revelar problemas críticos ou oportunidades ocultas? A detecção de anomalias ajuda a identificar dados que divergem significativamente do normal. Dados de séries temporais, ou seja, coletados ao longo do tempo, costumam incluir tendências e padrões sazonais. Ocorrem anomalias nesses dados quando esses padrões são rompidos, o que torna a detecção de anomalias uma ferramenta valiosa em setores como vendas, finanças, indústria e saúde.
Como dados de séries temporais têm características únicas, como sazonalidade e tendências, são necessários métodos especializados para detectar anomalias de forma eficaz. Nesta postagem de blog, vamos explorar alguns métodos populares de detecção de anomalias em séries temporais, incluindo a decomposição de STL e a previsão com LSTM, com exemplos detalhados de código para ajudar você a começar a usá-la.
Detecção de anomalias em séries temporais em empresas
Dados de séries temporais são essenciais em muitos ramos de atividade. Muitas empresas registram dados com marcações temporais, permitindo que mudanças sejam analisadas e que os dados sejam comparados ao longo do tempo. Séries temporais são úteis ao comparar uma certa quantidade ao longo de um certo período — por exemplo, comparações de um ano para o outro quando os dados têm características sazonais.
Monitoramento de vendas
Dados de vendas são um dos exemplos mais comuns de dados de séries temporais com diferenças sazonais. Como muitas vendas são afetadas pelos feriados anuais e pela época do ano, é difícil tirar conclusões sobre dados de vendas sem considerar as variações sazonais. Por isso, um método comum de analisar e encontrar anomalias em dados de vendas é a decomposição de STL, que abordaremos em detalhes mais adiante nesta postagem.
Finanças
Dados financeiros, como transações e preços de ações, são exemplos típicos de dados de séries temporais. No setor financeiro, é prática comum analisar e detectar anomalias nesses dados. Por exemplo, pode-se usar modelos de previsão de séries temporais em transações automáticas. Usaremos uma previsão de série temporal para identificar anomalias em dados de ações mais adiante nesta postagem.
Indústria
Outro caso de uso da detecção de anomalias em séries temporais é o monitoramento de falhas em linhas de produção. Máquinas costumam ser monitoradas, disponibilizando dados de séries temporais. É essencial poder notificar a administração sobre falhas em potencial e a detecção de anomalias desempenha um papel-chave nisso.
Medicina e saúde
Em Medicina e saúde, sinais vitais humanos são monitorados e pode-se detectar anomalias. Isso já é muito importante na pesquisa médica, mas é crítico no diagnóstico. Se um paciente hospitalizado tiver sinais vitais anômalos e não for tratado imediatamente, os resultados podem ser fatais.
Por que é importante usar métodos especiais na detecção de anomalias em séries temporais?
Dados de séries temporais são especiais, no sentido de que às vezes não podem ser tratados como outros tipos de dados. Por exemplo, se aplicarmos uma divisão de teste de treinamento a dados de séries temporais, a natureza sequencial desses dados significa que não podemos embaralhá-los. Isso também se aplica ao usarmos dados de séries temporais em modelos de aprendizado profundo. É comum usar uma rede neural recorrente (RNN) para levar em conta essa relação sequencial e os dados de treinamento são introduzidos como janelas de tempo, o que preserva a sequência de eventos dentro delas.
Dados de séries temporais também são especiais porque costumam ser sazonais e ter tendências que não podemos ignorar. Essa sazonalidade pode se manifestar em ciclos de 24 horas, 7 dias ou 12 meses, para citar apenas algumas possibilidades. Só podem ser determinadas anomalias depois de levar em conta a sazonalidade e as tendências, como você verá no nosso exemplo abaixo.
Métodos usados para a detecção de anomalias em séries temporais
Como dados de séries temporais são especiais, há métodos específicos para detectar anomalias neles. Dependendo do tipo dos dados, alguns dos métodos e algoritmos que mencionamos na nossa postagem anterior sobre detecção de anomalias podem ser usados em dados de séries temporais. Porém, com esses métodos, a detecção de anomalias pode não ser tão robusta quanto ao usar métodos projetados especificamente para dados de séries temporais. Em alguns casos, pode ser usada uma combinação de métodos de detecção para reconfirmar os resultados da detecção e evitar falsos positivos ou negativos.
Decomposição de STL
Uma das maneiras mais populares de usar dados sazonais de séries temporais é a decomposição de STL — sigla em inglês para “decomposição de tendências sazonais usando LOESS (suavização estimada localmente de gráficos de dispersão)”. Nesse método, decompõe-se uma série temporal usando uma estimativa da sazonalidade (com o período fornecido ou determinado através de um algoritmo), uma tendência (estimada) e um resíduo (o ruído nos dados). A biblioteca de Python statsmodels tem ferramentas para decomposição de STL.

Detecta-se uma anomalia quando o resíduo ultrapassa um determinado limiar.
Usando a decomposição de STL em dados de colmeias de abelhas
Em uma postagem anterior no blog, exploramos a detecção de anomalias em colmeias de abelhas usando os métodos OneClassSVM e IsolationForest.
Neste tutorial, vamos analisar dados de colmeias como uma série temporal, usando a classe STL, fornecida pela biblioteca statsmodels. Para começar, configure o seu ambiente usando o arquivo requirements.txt.
1. Instale a biblioteca
Já que vimos usando apenas o modelo fornecido pelo Scikit-learn, precisaremos instalar a biblioteca statsmodels a partir do PyPI. Isso é fácil de fazer no PyCharm.
Vá até a janela Python Packages (clique no ícone na parte inferior esquerda do IDE) e digite “statsmodels” na caixa de pesquisa.

Você pode ver todas as informações sobre o pacote no lado direito. Para instalá-lo, basta clicar em Install package.
2. Criação de um notebook do Jupyter
Para investigar o conjunto de dados mais a fundo, vamos criar um notebook do Jupyter para aproveitarmos as ferramentas do ambiente do PyCharm para esses notebooks.

Vamos importar o pandas e carregar o arquivo em .csv.
import pandas as pd
df = pd.read_csv('../data/Hive17.csv', sep=";")
df = df.dropna()
df

3. Inspeção dos dados como gráficos
Agora podemos inspecionar os dados como gráficos. Aqui, gostaríamos de ver a temperatura da colmeia 17 ao longo do tempo. Clique em Chart view no inspetor de dataframes e selecione T17 como o eixo Y nas configurações da série.

Quando expressa na forma de uma série temporal, a temperatura tem muitos altos e baixos. Isso indica um comportamento periódico, provavelmente devido ao ciclo de dias e noites. Portanto, pode-se presumir com confiança que há um período de 24 horas para a temperatura.
Depois, há uma tendência de queda da temperatura ao longo do tempo. Se você inspecionar a coluna DateTime, verá que as datas estão no período de agosto a novembro. Como a página de Kaggle do conjunto de dados indica que os dados foram coletados na Turquia, a transição do verão para o outono explica nossa observação de que a temperatura está caindo com o tempo.
4. Decomposição da série temporal
Para compreendermos a série temporal e detectarmos anomalias, faremos uma decomposição de STL, importando a classe STL da statsmodels e alimentando-a com nossos dados de temperatura.
from statsmodels.tsa.seasonal import STL stl = STL(df["T17"], period=24, robust=True) result = stl.fit()
Para a decomposição funcionar, teremos que informar um período. Como já mencionado, podemos presumir um ciclo de 24 horas.
Segundo a documentação, a classe STL decompõe uma série temporal em três componentes: de tendência, sazonal e residual. Para termos uma visão mais clara do resultado decomposto, podemos usar o método incorporado plot:
result.plot()

Você pode ver que os gráficos Trend e Season parecem se alinhar com nossas premissas acima. Porém, estamos interessados no gráfico residual, embaixo, que é a série original sem as alterações sazonais e de tendência. Qualquer valor residual extremamente alto ou baixo indica uma anomalia.
5. Limiar de anomalia
Agora, gostaríamos de determinar quais valores residuais consideraremos anormais. Para isso, podemos olhar o histograma dos valores residuais.
result.resid.plot.hist()

Esta pode ser considerada uma distribuição normal em torno de 0, com uma cauda longa acima de 5 e abaixo de −5. Então, vamos determinar um limiar de 5.
Para mostrar as anomalias na série temporal original, podemos colorir todas elas em vermelho no gráfico, assim:
import matplotlib.pyplot as plt
threshold = 5
anomalies_filter = result.resid.apply(lambda x: True if abs(x) > threshold else False)
anomalies = df["T17"][anomalies_filter]
plt.figure(figsize=(14, 8))
plt.scatter(x=anomalies.index, y=anomalies, color="red", label="anomalies")
plt.plot(df.index, df['T17'], color='blue')
plt.title('Temperatures in Hive 17')
plt.xlabel('Hours')
plt.ylabel('Temperature')
plt.legend()
plt.show()

Sem a decomposição de STL, é muito difícil identificar essas anomalias em uma série temporal que consista de períodos e tendências.
Previsão com LSTM
Uma outra maneira de detectar anomalias em dados de séries temporais é fazer uma previsão usando métodos de aprendizado profundo para estimar o desfecho de pontos de dados. Se uma estimativa for muito diferente do ponto real de dados correspondente, isso pode ser um sinal de dados anômalos.
Um algoritmo popular de aprendizado profundo para fazer previsões em dados sequenciais é o modelo “long short-term memory” (LSTM), um tipo de rede neural recorrente (RNN). Esse modelo tem portões de entrada, esquecimento e saída, que são matrizes numéricas. Isso garante que as informações importantes sejam passadas para a próxima iteração dos dados.

Como os dados de uma série temporal são sequenciais, o que significa que a ordem dos pontos de dados é sequencial e não deve ser embaralhada, o modelo LSTM de aprendizado profundo é eficaz para prever um desfecho em um determinado momento. Essa previsão pode ser comparada com os dados reais e pode-se determinar um limiar para decidir se os dados reais são anômalos.
Usando a previsão com LSTM em preços de ações
Agora, vamos criar um novo projeto do Jupyter para detectar quaisquer anomalias no preço das ações da Apple nos últimos 5 anos. O conjunto de dados de preços de ações contém os dados mais atualizados. Se você também quiser fazer isso para acompanhar esta postagem, pode baixar o conjunto de dados que estamos usando.
1. Criação de um projeto do Jupyter
Ao iniciar um novo projeto, você pode optar por criar um projeto do Jupyter, que é otimizado para ciência de dados. Na janela New Project, você pode criar um repositório de Git e determinar qual instalação do conda deve ser usada para gerenciar o seu ambiente.

Depois de criar o projeto, você verá um notebook de exemplo. Vá em frente e crie um novo notebook do Jupyter para este exercício.
Depois disso, vamos configurar o requirements.txt. Precisaremos do pandas, do matplotlib e do PyTorch, que é chamado de “torch” no PyPI. Como o PyTorch não está incluído no ambiente do conda, o PyCharm nos avisará que esse pacote está faltando. Para instalá-lo, clique no ícone da lâmpada e selecione Install all missing packages.

2. Carregamento e inspeção dos dados
Em seguida, vamos colocar nosso conjunto de dados apple_stock_5y.csv na pasta de dados e carregá-lo como uma dataframe do pandas para inspecioná-lo.
import pandas as pd
df = pd.read_csv('data/apple_stock_5y.csv')
df
Com a tabela interativa, podemos ver facilmente se está faltando algum dado.

Não há dados faltando, mas temos outro problema: gostaríamos de usar o preço Close/Last, mas seu tipo de dados não é numérico. Vamos fazer uma conversão e inspecionar nossos dados de novo:
df["Close/Last"] = df["Close/Last"].apply(lambda x: float(x[1:])) df
Agora podemos inspecionar o preço com a tabela interativa. Clique no ícone de gráfico à esquerda e será criado um gráfico. Como padrão, esse gráfico usará Date como o eixo X e Volume como eixo Y. Como gostaríamos de inspecionar o preço Close/Last, acesse as configurações clicando no ícone da engrenagem à direita e selecione Close/Last como o eixo Y.

3. Preparação dos dados de treinamento para LSTM
Agora, temos que preparar os dados de treinamento a serem usados no modelo de LSTM. Precisamos preparar uma sequência de vetores (a partir do eixo X), cada um representando uma janela de tempo, para prevermos o próximo preço. Este formará outra sequência (alvo no eixo Y). Aqui, podemos determinar a duração dessa janela de tempo através da variável lookback. O código a seguir cria as sequências de X e Y, que serão então convertidas em tensores do PyTorch:
import torch
lookback = 5
timeseries = df[["Close/Last"]].values.astype('float32')
X, y = [], []
for i in range(len(timeseries)-lookback):
feature = timeseries[i:i+lookback]
target = timeseries[i+1:i+lookback+1]
X.append(feature)
y.append(target)
X = torch.tensor(X)
y = torch.tensor(y)
print(X.shape, y.shape)
Em linhas gerais, quanto mais longa for a janela, maior será o nosso modelo, pois o vetor de entrada será maior. Porém, com uma janela mais longa, a sequência de entradas será menor. Portanto, a determinação dessa janela de “lookback” é um balanceamento. Vamos começar com 5, mas fique à vontade para experimentar outros valores e ver as diferenças.
4. Criação e treinamento do modelo
Podemos criar o modelo antes de treiná-lo usando o método nn module no PyTorch para criar uma classe. Esse método fornece blocos de construção, tais como diferentes camadas de redes neurais. Neste exercício, criaremos uma camada simples de LSTM, seguida de uma camada linear:
import torch.nn as nn
class StockModel(nn.Module):
def __init__(self):
super().__init__()
self.lstm = nn.LSTM(input_size=1, hidden_size=50, num_layers=1, batch_first=True)
self.linear = nn.Linear(50, 1)
def forward(self, x):
x, _ = self.lstm(x)
x = self.linear(x)
return x
Em seguida, treinaremos nosso modelo, mas antes disso, precisaremos criar um otimizador, uma função de perda usada para calcular a perda entre o valor real e o previsto de Y, e um carregador de dados para alimentar o modelo com nossos dados de treinamento:
import numpy as np import torch.optim as optim import torch.utils.data as data model = StockModel() optimizer = optim.Adam(model.parameters()) loss_fn = nn.MSELoss() loader = data.DataLoader(data.TensorDataset(X, y), shuffle=True, batch_size=8)
O carregador de dados pode embaralhar a entrada, pois já criamos as janelas de tempo. Isso preserva a relação sequencial em cada janela.
O treinamento é feito através de um loop for iterado para cada período. A cada 100 períodos, imprimiremos a perda e observaremos enquanto o modelo converge:
n_epochs = 1000
for epoch in range(n_epochs):
model.train()
for X_batch, y_batch in loader:
y_pred = model(X_batch)
loss = loss_fn(y_pred, y_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 != 0:
continue
model.eval()
with torch.no_grad():
y_pred = model(X)
rmse = np.sqrt(loss_fn(y_pred, y))
print(f"Epoch {epoch}: RMSE {rmse:.4f}")
Começamos com 1000 períodos, mas o modelo converge bem rapidamente. Fique à vontade para experimentar outros números de períodos no treinamento, para obter o melhor resultado.
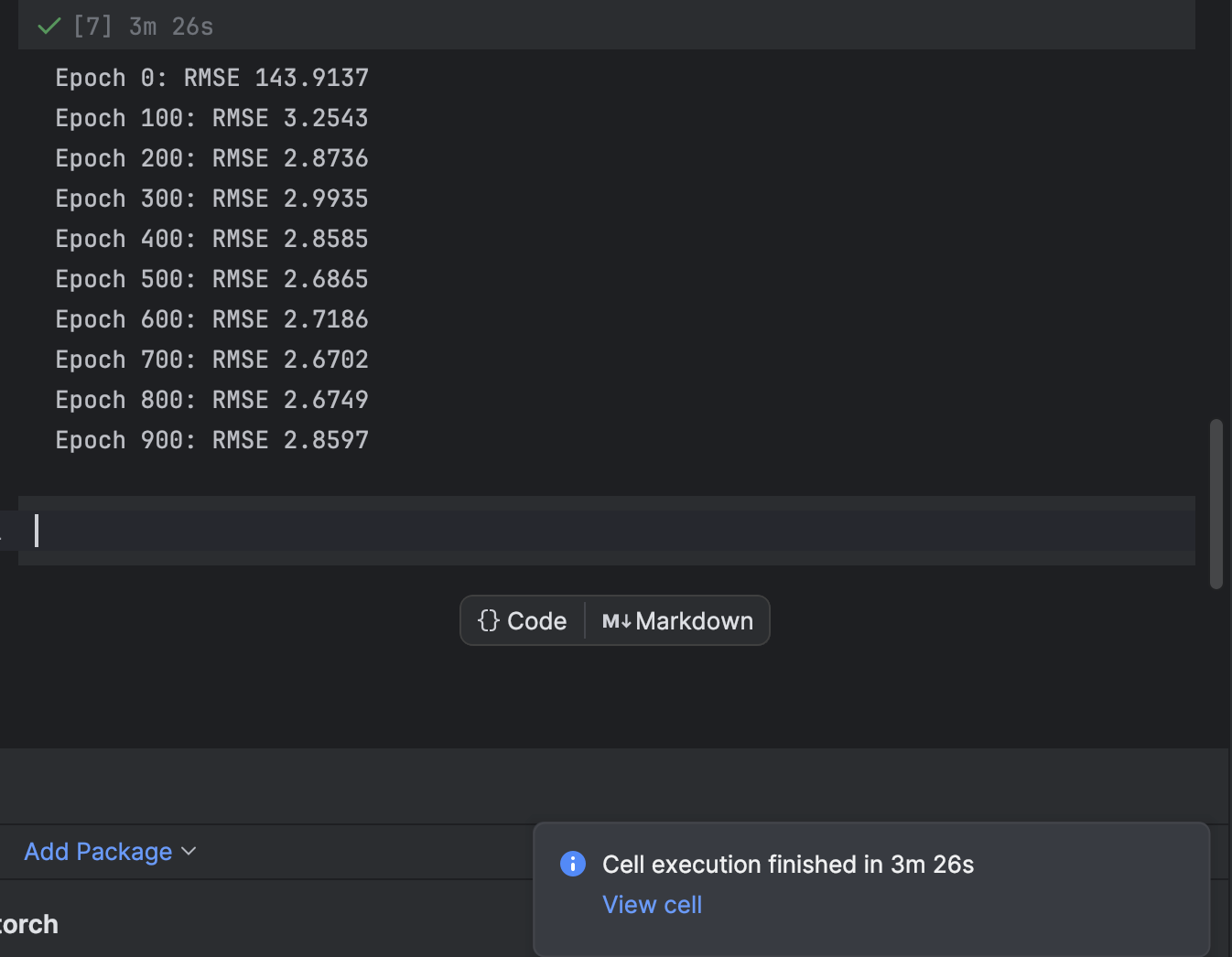
No PyCharm, uma célula que demore algum tempo para ser executada mandará uma notificação de quanto tempo falta e dará um atalho para a célula. Isso é muito útil ao treinar modelos de aprendizado de máquina, especialmente de aprendizado profundo, em notebooks do Jupyter.
5. Criação de um gráfico da previsão e localização de erros
Depois, vamos criar a previsão e fazer um gráfico dela, juntamente com a série temporal real. Observe que teremos que criar uma série 2D np para coincidir com a série temporal real. Esta aparecerá em azul, enquanto a série prevista aparecerá em vermelho.
import matplotlib.pyplot as plt
with torch.no_grad():
pred_series = np.ones_like(timeseries) * np.nan
pred_series[lookback:] = model(X)[:, -1, :]
plt.plot(timeseries, c='b')
plt.plot(pred_series, c='r')
plt.show()

Se você observar com atenção, verá que a previsão e os valores reais não se alinham perfeitamente. Porém, a maioria das previsões é razoável.
Para inspecionar os erros mais de perto, podemos criar uma série dos erros e usar a tabela interativa para observá-los. Desta vez, vamos usar o erro absoluto.
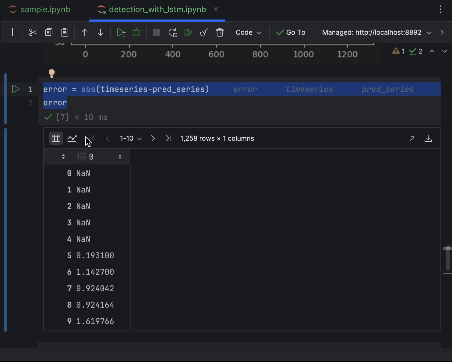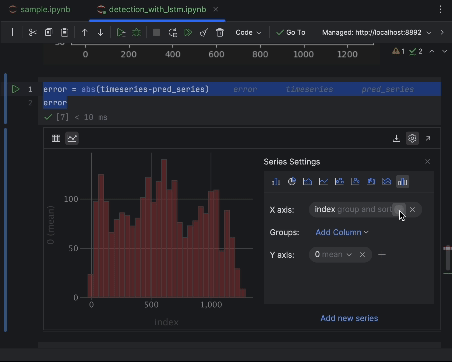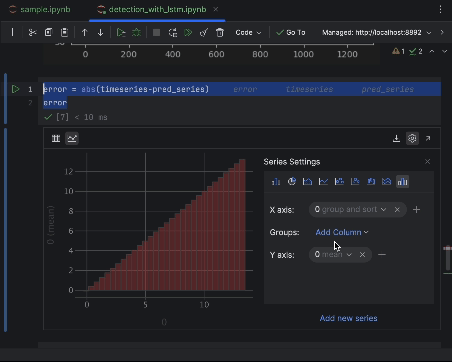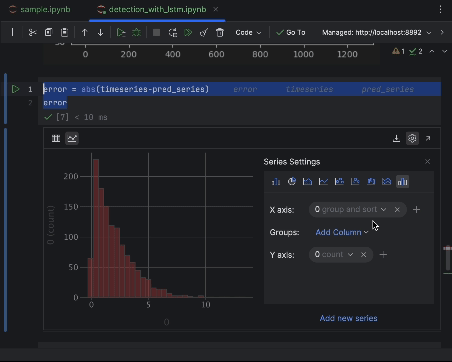
error = abs(timeseries-pred_series) error
Use as configurações para criar um histograma com o valor do erro absoluto como o eixo X e a contagem do valor como o eixo Y.
6. Determinação do limiar de anomalia e visualização
A maioria dos pontos terá um erro absoluto de menos de 6. Portanto, podemos determinar esse valor como o limiar de anomalia. De forma semelhante ao que fizemos com as anomalias na colmeia, podemos traçar os pontos de dados anômalos no gráfico.
threshold = 6
error_series = pd.Series(error.flatten())
price_series = pd.Series(timeseries.flatten())
anomalies_filter = error_series.apply(lambda x: True if x > threshold else False)
anomalies = price_series[anomalies_filter]
plt.figure(figsize=(14, 8))
plt.scatter(x=anomalies.index, y=anomalies, color="red", label="anomalies")
plt.plot(df.index, timeseries, color='blue')
plt.title('Closing price')
plt.xlabel('Days')
plt.ylabel('Price')
plt.legend()
plt.show()

Resumo
É comum usar dados de séries temporais em muitas aplicações, inclusive de negócios e de pesquisa científica. Devido à natureza sequencial desses dados, usam-se métodos e algoritmos especiais para ajudar a detectar anomalias neles. Nesta postagem de blog, demonstramos como identificar anomalias usando a decomposição de STL para eliminar a sazonalidade e as tendências. Também demonstramos como usar o aprendizado profundo e o modelo LSTM para comparar a estimativa prevista com os dados reais, com a finalidade de detectar anomalias.
Detecte anomalias com o PyCharm
Com um projeto do Jupyter no PyCharm Professional, você pode facilmente organizar a sua detecção de anomalias, usando diversos arquivos de dados e notebooks. Podem ser gerados gráficos de saída, muito acessíveis no PyCharm, para inspecionar anomalias. Outros recursos, como sugestões de complementação automática, tornam muito fácil a navegação pelos modelos do Scikit-learn e configurações de gráficos da Matplotlib.
Incremente os seus projetos de ciência de dados usando o PyCharm e confira os recursos que ele oferece para otimizar o seu fluxo de trabalho em ciência de dados.
Artigo original em inglês por:
Subscribe to PyCharm Blog updates







